2. 멀쩡한 사각형

문제 설명

가로 Wcm, 세로 Hcm의 직사각형 종이가 있다. 이때 격자가 1cm*1cm크기로 생성되어 있다.

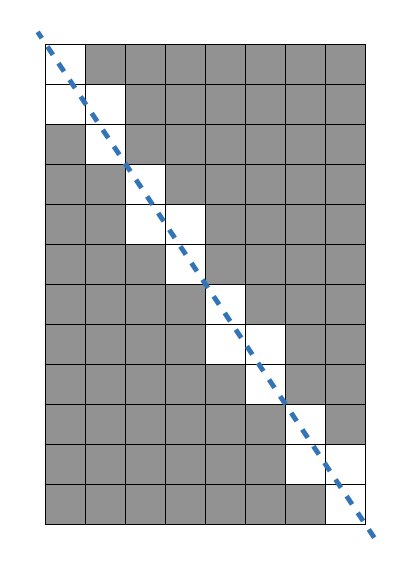
근데 이때 직사각형의 한 꼭지점에서 대각에 위치한 꼭지점까지 직각삼각형으로 잘리게 되었다.

이때 제대로된 격자 사각형 (1*1)이 아니면 사용할 수 없다. 그렇다면 사용가능한 격자 사각형의 개수는?

Inputs

Variable Name	type	meaning
W	Int	width
H	Int	height

output

return Long // total number of available 1*1 squares.

Conditions

W & H
- value: ~ 1억

Test cases

W	H	result
8	12	80

Solution

이 문제 파이썬으로 어떻게 풀었었는 지 보지 말고 풀자.

Idea1

일단 W, H를 1 by X로 변환해보자. (X ≥ 1)

예시의 경우, (W, H) = (8. 12) → (W’, H’) = (1, 1.5) , 변환 계수 K = 8

1 by 1.5의 경우 1 by 2의 사각형에서 2개를 사용못한다. (1.5 → round)

1 by 2에서 2개 사용불가 → 계수 K는 8 고로 16개 사용불가

전체 격자 개수: 96개

사용 가능 개수: 96 - 16 = 80

def solution(w: Int, h: Int): Long = {
  val convertConstant = (w).min(h)
  val unavailable = math.ceil((w).max(h).toDouble / convertConstant).toInt

  val totalBox = w.toLong * h.toLong

  return totalBox - unavailable * convertConstant
}

실패. 5*3같은 상황에서 이상하게 계산한다.

Idea2

맨 처음에 생각했던 최대 공약수로 계산해야하는 게 맞는 거 같긴한데

예시의 경우, (W, H) = (8. 12) → (W’, H’) = (2, 3) , 변환 계수 K = 4

2 by 3의 경우 4개를 사용못한다. 이거 어떻게 계산하지?

1by 1.5 → 2칸

1.5 by 1 → 2칸

이렇게 계산해야하나?

그러면 5*3은?

1by(0~5/3) → 1by(0~2) → 2칸
1by(5/3~10/3) → 1by(1~4) → 3칸
1by(10/3~5) → 1by(3~5) → 2칸

이렇게 계산해야겠다.

def gcd(a: Long, b: Long): Long = if(b == 0) a else gcd(b, a%b)
def solution(w: Int, h: Int): Long = {
  val width = w.toLong
  val height = h.toLong

  val convertK = gcd(width, height)

  val smallCell = Vector[Long](width/convertK, height/convertK)
  val cell_small = smallCell.min
  val cell_large = smallCell.max
  val ratio = cell_large.toDouble / cell_small.toDouble

  val cellUnavailable = (1 to cell_small.toInt)
  .map(row => 
       math.ceil(ratio*row) - math.floor(ratio*(row-1))
      ).sum.toLong

  return width*height - cellUnavailable*convertK
}

테케 두개를 틀린다… 뭐지 변수 range 문제인가

Edge case handling

ratio를 먼저 계산해서 저장한게 변수 범위 문제를 일으켰다.

val ratio = cell_large.toDouble / cell_small.toDouble

val cellUnavailable = (1 to cell_small.toInt)
  .map(row => 
       math.ceil(ratio*row) - math.floor(ratio*(row-1))
      ).sum.toLong

이부분을 다음과 같이 바꿔야한다.

val cell_large = smallCell.max
        
val cellUnavailable = (1 to cell_small.toInt)
.map(row => 
     math.ceil(row.toLong * cell_large.toDouble / cell_small.toDouble)
     - math.floor((row-1).toLong * cell_large.toDouble / cell_small.toDouble)
    ).sum.toInt

Study from Implementation

올림 함수 ceil도 math에 있다.
- math.ceil로 사용
버림은
- floor
static 변수 선언 언어다. 변수 사용시 범위에 유의해서 사용하자.